Resolución de Problemas con Fracciones - Curso de Razonamiento Numérico

Tema 3: Problemas con Fracciones.

3.1. Ejemplos de Resolución de Problemas con Fracciones.

1. En un salón hay 24 hombres y 12 mujeres. ¿Qué parte del salón son las mujeres?
2. En una balanza se coloca, en un lado, una pesa de 2 1/4 kg, y en el otro 3/4 kg. ¿Cuánto falta para equilibrar la balanza?
3. ¿Cuántos paquetes de 1/4 kg de mantequilla se necesitan para tener 3 kg?
4. ¿Qué parte del día ha transcurrido a las 3 pm?
5. Fernando estudia 1/8 del día. ¿Cuántas horas estudia Fernando?

Resolución de Problemas con Sistema de Ecuaciones - Curso de Razonamiento Numérico

Tema 2: Ecuaciones y Problemas

2.4. Resolución de Problemas mediante un Sistema de Ecuaciones de Primer Grado.

2.4.1 Métodos de solución para un Sistema de Ecuaciones 2x2.
Para resolver un sistema de ecuaciones lineales tenemos los siguientes métodos:
1) Métodos Algebraicos. 
   - Método de Igualación.
   - Método de Sustitución.
   - Método de Eliminación.
2) Método Gráfico.


2.4.2 Problemas Resueltos.
Problema 1
En una granja entre gallinas y cerdos se cuentan 100 patas y 35 cabezas. ¿Cuántos cerdos hay en la granja?
A) 15        B) 20      C) 25      D) 30       E) 35



Problema 2
De dos números que suman 240,  uno de ellos es el cuádruple del otro. Calcular el triple de la sexta parte del menor.
A) 48      B) 16       C) 42       D) 24       E) 8

Problema 3
Si tengo como mascotas: perros, gatos y canarios y además si todos son perros menos 8, todos son gatos menos 5, y todos son canarios menos 7, ¿cuántos perros tengo?
A) 2          B) 3         C) 4          D) 5

Resolución de Problemas con Ecuaciones - Curso de Razonamiento Numérico

Tema 2: Ecuaciones y Problemas

2.3. Resolución de Problemas mediante Ecuaciones de Primer Grado con una Incógnita.

2.3.1 Método para plantear una ecuación.
Para resolver un problema, recomendamos seguir los siguientes pasos:
1) Identificar a la incógnita. 
2) Definir algunas variables que nos permita traducir la expresión verbal del problema a la forma simbólica (expresión matemática).
3) Resolver la ecuación (o ecuaciones) resultantes. 
4) Dar respuesta a la incógnita.




2.3.2 Problemas Resueltos.
Problema 1
Juan tiene los 5/6 de lo que tiene Pedro. Si Juan recibe $80 de Pedro, éste tiene los 2/5 de lo que tiene Juan. ¿Cuánto tiene Pedro?
A) $ 140       B) $ 120         C) $ 138       D) $ 168


Problema 2
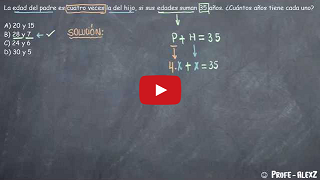
La edad del padre es cuatro veces la del hijo, si sus edades suman 35 años. ¿Cuántos años tiene cada uno?
A) 20 y 15      B) 28 y 7        C) 24 y 6       D) 30 y 5

Problema 3
La suma de tres números impares consecutivos es igual a 99. Halle la suma de los dos números mayores.

A) 68

B) 69

C)65

D) 70

E) 66

Problema 4
Hallar cuatro números cuya suma sea 90. El segundo es el doble del primero, el tercero es el doble del segundo y el cuarto es el doble del tercero. ¿Cuáles son los números?
A) 8, 16, 32, 64     B) 5, 10, 20, 40     C) 6, 12, 24, 48     D) 10, 20, 40, 20

Resolución de Ecuaciones - Curso de Razonamiento Numérico

Tema 2: Ecuaciones y Problemas

2.2. Resolución de Ecuaciones.

2.2.1 Ecuaciones de Primer Grado con una Incógnita.
Al resolver una ecuación, en necesario aplicar las propiedades de las operaciones y algunas de las propiedades de la igualdad en el conjunto de los números reales.




► Práctica 1

Lenguaje Algebraico - Curso de Razonamiento Numérico

Tema 2: Ecuaciones y Problemas

2.1. Lenguaje Algebraico.

2.1.1 ¿Qué es lenguaje algebraico?

El lenguaje algebraico relaciona números y letras mediante los simbolos de las operaciones matemáticas. La principal función de lenguaje álgebraico es estructurar un idioma que ayude a generalizar las diferentes operaciones que se desarrollan dentro de la aritmética.

☆ Ejemplos Resueltos

 

Lenguaje Algebraico
Lenguaje Común	Lenguaje Algebraico
Un número par cualquiera.	2x
Un número cualquiera aumentado en siete.	x + 7
La diferencia de dos números cualesquiera.	x - y
El doble de un número excedido en cinco.	2x + 5
La división de un número entero entre su antecesor	x/(x-1)
La mitad de un número.	d/2
El cuadrado de un número	x2
La semisuma de dos números	(x+y)/2
Las dos terceras partes de un número disminuidos en cinco es igual a 12.	2/3 (x-5) = 12
Tres números naturales consecutivos.	x, x + 1, x + 2.
La parte mayor de 1200, si la menor es w	1200 - w
El cuadrado de un número aumentado en siete.	a2 + 7
Las tres quintas partes de un número más la mitad de su consecutivo equivalen a tres.	3/5 p + 1/2 (p+1) = 3
El producto de un número positivo con su antecesor equivalen a 30.	x(x-1) = 30
El cubo de un número más el triple del cuadrado de dicho número.	x3 + 3x2
El doble de la diferencia de dos números.	2(x - y)
El triple de la suma de dos números.	3(x + y)
El denominador de una fracción, es cinco unidades menor que su numerador.	x/(x - 5)
En un terreno de forma rectangular, su ancho mide la mitad de su largo.	a = L/2
El ancho de un rectángulo es igual a las tres cuartas partes de su longitud.	a = 3/4 L
El numerador de una fracción excede al denominador en tres unidades.	(x+3)/x
La suma de tres números consecutivos.	x + (x+1) + (x+2)
El doble de la tercera potencia de x.	2x3

Números Decimales - Curso de Razonamiento Numérico

Tema 1: Números y Operaciones

1.4. Números Decimales.

1.4.1 ¿Qué son los números decimales?

Se denominan números decimales aquellos que poseen una parte decimal, en oposición a los números enteros que carecen de ella. La parte entera corresponde a un número entero (es decir que puede ser cero, o un número negativo); la parte decimal o fraccionaria, corresponde al valor decimal situado entre cero y uno.

1.4.2 Suma y resta de números decimales

Para sumar  o restar números decimales, escribimos uno debajo del otro de modo que las unidades del mismo orden estén  en la misma columna. Si los números no tienen igual cantidad de cifras decimales, agregamos los ceros necesarios a la derecha. Al resultado le colocamos la coma decimal en el lugar correspondiente.

Números Racionales - Curso de Razonamiento Numérico

Tema 1: Números y Operaciones

1.3. Números Racionales (Fracciones).

1.3.1 ¿Qué son los números racionales?
Se llama número racional a todo número que puede representarse como el cociente de dos números enteros o, más precisamente, un entero y un natural positivo, es decir, una fracción común a/b con numerador a y denominador b distinto de cero. El término «racional» alude a fracción o parte de un todo.
¿Qué son las fracciones?