Lenguaje Algebraico - Curso de Razonamiento Numérico

Tema 2: Ecuaciones y Problemas

2.1. Lenguaje Algebraico.

2.1.1 ¿Qué es lenguaje algebraico?

El lenguaje algebraico relaciona números y letras mediante los simbolos de las operaciones matemáticas. La principal función de lenguaje álgebraico es estructurar un idioma que ayude a generalizar las diferentes operaciones que se desarrollan dentro de la aritmética.

☆ Ejemplos Resueltos

 

Lenguaje Algebraico
Lenguaje Común	Lenguaje Algebraico
Un número par cualquiera.	2x
Un número cualquiera aumentado en siete.	x + 7
La diferencia de dos números cualesquiera.	x - y
El doble de un número excedido en cinco.	2x + 5
La división de un número entero entre su antecesor	x/(x-1)
La mitad de un número.	d/2
El cuadrado de un número	x2
La semisuma de dos números	(x+y)/2
Las dos terceras partes de un número disminuidos en cinco es igual a 12.	2/3 (x-5) = 12
Tres números naturales consecutivos.	x, x + 1, x + 2.
La parte mayor de 1200, si la menor es w	1200 - w
El cuadrado de un número aumentado en siete.	a2 + 7
Las tres quintas partes de un número más la mitad de su consecutivo equivalen a tres.	3/5 p + 1/2 (p+1) = 3
El producto de un número positivo con su antecesor equivalen a 30.	x(x-1) = 30
El cubo de un número más el triple del cuadrado de dicho número.	x3 + 3x2
El doble de la diferencia de dos números.	2(x - y)
El triple de la suma de dos números.	3(x + y)
El denominador de una fracción, es cinco unidades menor que su numerador.	x/(x - 5)
En un terreno de forma rectangular, su ancho mide la mitad de su largo.	a = L/2
El ancho de un rectángulo es igual a las tres cuartas partes de su longitud.	a = 3/4 L
El numerador de una fracción excede al denominador en tres unidades.	(x+3)/x
La suma de tres números consecutivos.	x + (x+1) + (x+2)
El doble de la tercera potencia de x.	2x3

---

2.1.2 Problemas de Entrenamiento para el ENES.

Objetivo: llegar a resolver cada problema en menos de un minuto.

NIVEL BÁSICO.
Expresar en lenguaje algebraico los siguientes enunciados:

1. La mitad de un número, aumentado en su doble.
A) x/2       B) x²          C) 2x        D) x/2 + 2x

2. El doble de un número más su tercera parte.
A) 2x + 3         B) 2(x + 3)     C) 2x + x/3        D) x/2 + 3    

3. La mitad del triple de un número menos cuatro.
A) 3x - 4        B) 3x/2 - 4        C) x - 3·4       D) (3x - 4)/2

4. El triple de la mitad del cubo de un número.
A) 3x/2        B) 3/2x       C) 3x³/2       D) 3x³

5. Siete menos el doble del cuadrado de un número.
A) 7 - 2x       B) 2x² - 7        C) 7 - 2x³        D) 7 - 2x²

6. El doble de la suma de dos números consecutivos.
A) 2(2x+1)       B) 2x + x      C) 2(x + x)       D) 2(x + 2x)

7. El triple de la suma de tres números.
A) a + b + c · 3      B) 3 + a + b + c        C) 3(a + b + c)       D) 3·a + b + c  

8. La edad de una persona hace cinco años.
A) 32 - 5        B) 5 - x          C) x - 5        D) 2x - 5

9. El antecesor del número natural 3(x – 1).
A) 3x     B) 3x – 3     C) 3x – 2     D) 3x – 4

10. La diferencia del cubo de un número menos su mitad"
A) (x² - x)/2        B) x³ - x/2        C) (x³ - x)/2         D) x³ - 1/2

11. Un numero de 3 cifras con x unidades, y decenas y z centenas"
A) xyz        B) yxz        C) yzx       D) zyx

12. ¿Cuál de las siguientes expresiones representa un número que tiene a unidades menos que el número n?
A) a – n     B) n : a     C) n – a      D) a : n

13. El papá de José tenía x años cuando él nació. Si ahora José tiene y años. ¿Qué edad tendrá el papá en y años más?
A) 2y       B) x + 2y      C) 2x + y      D) x – 2y

14.  Al número h se le suma m, dicha suma se divide por k y el resultado se multiplica por p.
A) (h + m/k)·p   
B) (h + m·p)/k
C) [(h + m)/k]·p
D) h/k + m·p   

15.  El cuadrado de la diferencia de dos numeros equivale al cociente de su suma entre su diferencia"
A) (x² – y²) = (x – y)/(x + y)
B) (x² – y²) = (x + y)/(x – y)
C) (x – y)² = (y + x)/(y – x)
D) (x – y)² = (x + y)(x – y)

Respuestas ✔  1) D       2) C       3) D       4) C       5) D
  6) A       7) C       8) C       9) D      10) B
11) D     10) C     11) B      12) C      13) B
14) C     15) D 



NIVEL INTERMEDIO
Problema 1
Si n es un número impar, entonces el sucesor impar del sucesor de n+1 se representa por
A) 2n      B) n + 3       C) 3n + 4     D) n + 4

Problema 2
"La semidiferencia entre a y  b, disminuido en el triple de  a", se expresa por
A) (a - b)/2 - 3a
B) (a - b)- 3b
C) (a - b) - 3
D) (a - b)/2 - 3

Problema 3
Al escribir en lenguaje algebraico “el cuadrado de la diferencia entre el triple de a y el doble de b” resulta:
A) 3a – 2b²         B) (3a – b²)        C) (3a – 2b)²       D) b² – 3a

Problema 4
El cubo del doble de la diferencia de p y q”, se representa por:
A) 2(p³ – q³)
B) 2(p – q)³
C) (2p – 2q)³
D) [2(p – q)]³

Problema 5
Si al cuádruplo del antecesor de w se le suma el sucesor del sucesor de w y al resultado se le resta el triple de w, resulta
A) 2(w + 1)          B) 2(w – 1)         C) (w – 6)        D) 2(w + 6)

Problema 6
Si m es un número entero impar, el número impar antecesor de 3m + 6 es:
A) 3m
B) 3m + 8
C) 3m + 7
D) 3m + 5

Problema 7
El enunciado: “el cuadrado de la suma de dos números x  y  y es igual al doble de la diferencia de los cuadrados de esos números”, se expresa:
A) x² + y² = 2(x – y)²              B) x² + y² = 2(x²– y²)
C) (x + y)² = 2(x – y)²             D) (x + y)² = 2(x²– y²)

Problema 8
El sueldo mensual de una persona es $ M. Si gasta las tres cuartas partes y el resto lo ahorra, ¿cuál de las siguientes expresiones representa el ahorro trimestral de dicha persona?
A) M - 1/4
B) (M - 3/4M)
C) 3M - 1/4
D) 3(M - 3/4M)

Problema 9
Carlos compra un DVD a crédito en 5B dólares,  pagando un  tercio al contado y el resto en seis cuotas iguales. ¿Cuál es el valor en dólares de cada cuota?
A) 10/3B
B) 5B - 2/3
C) 5/9B
D) 5/6B - 2/3B

Problema 10
Si la edad de una persona en y años más será x años, ¿cuántos años tiene?
A) y
B) x + y
C) x - y
D) x

Problema 11
Durante la evaluación de un examen cada pregunta se debe contestar en un tiempo máximo de m minutos; si el examen consta de n preguntas, ¿cuál debería ser la duración máxima del examen medida en horas?
A) 60(m·n)
B) 60(m + n)
C) (m·n)/60
D) 60/(m + n)

Problema 12
Un rollo de listón de m-1 metros se va a dividir en n+1 tramos iguales, ¿qué fracción de metro medirá cada uno de los tramos?
A) m/n
B) (m+1)/(n+1)
C) (n+1)/(m-1)
D) (m-1)/(n+1)

Problema 13
La edad de Juanito hace b años fue c años, ¿cuántos años tendrá dentro de d años?
A) c - b + d
B) b - c + d
C) b - c - d
D) b + c + d

Problema 14
¿Cuántos segundos hay en m minutos y s segundos ?
A) 60m + s
B) m + 60s
C) 60(m + s)
D) (m + s)/60

Problema 15
Si en la granja M hay 8 vacas más que en la granja H, y a su vez la granja P tiene 12 vacas mas que la H. Si x representa la cantidad de vacas en la granja H, ¿cuál es la expresión algebraica que representa la cantidad total de vacas en las tres granjas?
A) 20 + x        B) 3x + 12        C) 20 + 3x        D) 3x + 8

Problema 16
Un padre reparte $k entre sus tres hijos. Si al mayor le corresponde 2/5 del dinero y al segundo los 2/3 del resto, ¿cuánto le corresponde al menor?
A) $ 6/15k
B) $ 2/3k
C) $ 3/5k
D) $ k/5

Problema 17
Una persona gana $m mensual y gasta $s semestral. ¿Cuánto logra ahorrar en un trimestre?
A) 3m + s/2       B) (3m + s)/2        C) 3m – s/2        D) (3m – s)/2

Problema 18
Antonio es menor que Lucía por 3 años, Lucía es mayor que Judith por 7 años. Si x representa la edad de Antonio en años. ¿Cuál es la edad de Judith?
A) x + 3
B) x - 3
C) x - 4
D) x - 7

Problema 19
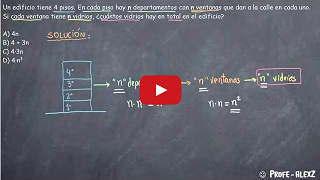
Un edificio tiene 4 pisos. En cada piso hay n departamentos con n ventanas que dan a la calle en cada uno. Si cada ventana tiene n vidrios, ¿cuántos vidrios hay en total en el edificio?
A) 4n       B) 4 + 3n        C) 4·3n        D) 4·n

Problema 20
Alberto realiza una tarea en m días y Bruno realiza la misma tarea en n días. ¿Cuánto demorarán si trabajan juntos?
A) (m + n)/mn
B) m/n
C) mn/(m + n)
D) m + n