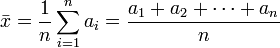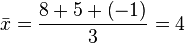Todo lo que necesitas saber sobre el ENES
Preguntas frecuentes.
1. ¿Para qué sirve el SNNA?
El Sistema Nacional de Nivelación y Admisión sirve para que todos los bachilleres puedan estudiar la carrera que elijan, en cualquier universidad pública. Es un proceso que elimina el favoritismo que existía anteriormente.
2. ¿Qué es el ENES?
El Examen Nacional de Educación Superior, o ENES, es una herramienta que evalúa tus habilidades y capacidades para resolver problemas de la vida cotidiana. Con los resutados del ENES tú puedes postular a los cupos de las carreras que quieres estudiar.
3. ¿Qué es una IES?
Una IES es como se conoce a toda Institución de Educación Superior del Ecuador.
4. ¿Cómo me registro para dar el ENES?
Tienes que registrarte en la página www.snna.gob.ec
5. ¿La SENESCYT me escoge la carrera?
No, tú eliges la carrera de acuerdo a tus intereses. Tienes 5 opciones y puedes escoger todas las carreras relacionadas a una misma área de estudios, en diferentes universidades.
6. ¿Cuál es el puntaje mínimo que debo obtener en el ENES?
La calificación para acceder a un cupo de nivel superior partirá de una base de 800/1 000 para Medicina y Ciencias de la Educación, y a partir de 600/1
000 puntos para que el aspirante pueda postular a las demás carreras.
7. ¿Es necesario dar otra vez el ENES para cambiarte de Universidad?
No, solo debes tramitar el reconocimiento de los créditos que has aprobado en la Universidad a la que quieres cambiarte.
8. ¿Si estoy en la universidad, puedo aplicar a una beca a través del ENES?
Las IES públicas te garantizan educación gratuita. Si quieres acceder a una beca y estudias en una Universidad privada, debes acercarte al departamento de Bienestar estudiantil o averiguar la oferta de becas del IECE.
9. ¿Se toma a consideración las notas del bachillerato o no?
No, tus calificaciones del colegio no son tomadas en cuenta, solo importa el puntaje que consigas en el ENES.
10. ¿Si estoy en una Universidad puedo cambiarme a otra?
Sí, siempre y cuando seas estudiante regular de una Universidad. Luego debes seguir el proceso de acuerdo a las normas de cada Universidad.
11. ¿Qué es la oferta académica?
La oferta académica son las carreras y cupos disponibles de cada IES. La oferta académica la puedes revisar en la página web del SNNA (http://www.snna.gob.ec/) al inicio de cada proceso de admisión.
12. ¿Las preguntas del ENES son capciosas?
No lo son. Las preguntas están diseñadas para identificar como resuelves problemas de forma lógica y analítica. Cuando te inscribes en el SNNA puedes responder un examen simulador del ENES para que practiques y conozcas cómo funciona.
13. ¿Para qué universidades hay que dar el ENES?
Para las Universidades públicas es obligatorio. Si quieres estudiar en una Universidad privada, puedes hacerlo con el ENES o con el proceso de cada institución.
14. ¿Cuál es el rango de edad para dar el ENES?
No hay ningún límite de edad, solo debes haber terminado el colegio o estar cursando el último año.
15. ¿Cómo puedo repasar las preguntas del ENES?
Una vez inscrito en el SNNA encontrarás un simulador del examen en la página Web. En éste blog tambien encontrarás bastante material para repasar.










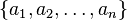 , la media aritmética se define como:
, la media aritmética se define como: